 Knowing how to find both charge and isoelectric point for amino acids is a critical MCAT skill. Understanding why an amino acid will gain or lose a proton at a given pH is even more critical.
Knowing how to find both charge and isoelectric point for amino acids is a critical MCAT skill. Understanding why an amino acid will gain or lose a proton at a given pH is even more critical.
The MCAT is a test of logic and understanding, which is why this article will break down amino acid charge and calculations from a logical application perspective.
While the math concept may be tricky at first, you’ll find that once it makes sense, it’s fairly easy to apply these critical skills for the MCAT.
When you think of amino acid charge, the first related topic that comes to mind is isoelectric point.
What is an isoelectric point?
The word isoelectric or isoelectronic comes from ‘iso,’ which means the same, and ‘electric,’ which implies charge. The isoelectric point or pI of an amino acid is the pH at which an amino acid has a net charge of zero.
Looking at this standard drawing of an amino acid, it appears to be neutral–how does that relate to the pl?

This drawing is simplified, and is actually incorrect.
At physiological pH, amino acids will exist with a net charge of zero. That’s not because they have no charge: it’s because their charges balance or cancel out.
What is a Zwitterion?
Zwitterion comes from the German word for ‘two’ (zwei) or ‘double’ (zwitter) and the word ‘ion’. While neutral, the zwitterion form of an amino acid will have a positive and a negative charge.
This is the zwitterion form of an amino acid
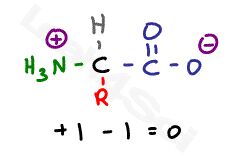
The standard structure contains both a carboxyl and an amine in the backbone. Acidic and basic amino acids may have additional groups in their side chains.
(Learn more about amino acid side chains link)
Finding Charge on a Carboxyl Group
Let’s compare the carboxyl and amine groups to simple molecules like acetic acid and methyl amine. If you find your acid/base knowledge weak, start by reviewing my acid/base video series, reading this (link) acid/base overview article, and downloading my free acid/base cheat sheet.
 A carboxylic acid in solution will exist in equilibrium with carboxylate or acetate, its conjugate base. Disregard the complex ICE charts for calculating dissociation; instead, look at what drives this reaction towards the right or left.
A carboxylic acid in solution will exist in equilibrium with carboxylate or acetate, its conjugate base. Disregard the complex ICE charts for calculating dissociation; instead, look at what drives this reaction towards the right or left.

If we lower the pH of a solution by adding a strong acid like HCl, there will be an abundance of H+ in the solution. These free H+ ions will protonate any free acetate ions in solutions thus favoring the product of this equilibrium reaction. According to Le Chatelier’s principle, if product is added, the system will shift to the left to reestablish equilibrium. The reaction now favors the protonated acetic acid form.

As the pH is increased with the addition of a strong base like sodium hydroxide (NaOH), the equilibrium will now shift to the right. Since the OH- will react with the free H+ in solution to form water, Le Chatelier’s principle says the reaction must shift to the right to reform that H+. As the pH increases, equilibrium will continue to shift to the right, favoring the deprotonated acetate form over the protonated acetic acid. 
What is the turning point of this equilibrium?
Since acetic acid is considered a weak acid (strong within the scale of weak acids), there is a range at which the acetic acid and acetate will form a stable buffer.

 Using the Henderson-Hasselbalch equation for buffers, it’s possible to calculate the pH based on the ratio of acid to conjugate base, or calculate the ratio given the pH and pKa value. You REALLY don’t want to waste time with calculations like this on the MCAT.
Using the Henderson-Hasselbalch equation for buffers, it’s possible to calculate the pH based on the ratio of acid to conjugate base, or calculate the ratio given the pH and pKa value. You REALLY don’t want to waste time with calculations like this on the MCAT.
That’s where my Henderson Hasselbalch trick comes in handy, as explained in the video below.
Finding Charge for a Protonated Amine
 Now let’s take a look at a simple base like methylamine. Methylamine is amphiprotic, meaning that it can donate or accept a proton thus acting as an acid or a base.
Now let’s take a look at a simple base like methylamine. Methylamine is amphiprotic, meaning that it can donate or accept a proton thus acting as an acid or a base.
Since we’re comparing methylamine to the amino group on the amino acid, we’re only interested in its ability to accept a proton and form a conjugate acid.
In fact, since you are provided with pKa acid values, we have to look at this molecule as the reaction between the protonated amine and its deprotonated conjugate base methylamine.

The pKa value given for the amino group on any amino acid specifically refers to the equilibrium between the protonated positive nitrogen and deprotonated neutral nitrogen. You’ll never see a neutral nitrogen deprotonated to form a negative on an amino acid.

The pKa of the protonated methylamine conjugate acid is like this: at physiological pH, there is an abundance of free H+ in the solution, which shifts equilibrium to the left, to the protonated positive nitrogen.
As the pH rises towards the pKa value, there will be deprotonation. At the pKa value, there will be a 50/50 mix of protonated and deprotonated molecules in a perfect buffer (see video above). As the pH continues to rise, more and more molecules will deprotonate till the neutral uncharged form dominates.
Finding Charge on Amino Acids in Preparation for Isoelectric Point Calculations
While we started by analyzing acetic acid and methylamine independently, the same concept applies when analyzing the amino and carboxyl groups on an amino acid. The key is to tackle each acid/base side chain individually to determine its charge, then analyze the molecule as a whole, and FINALLY summing charges for an overall net charge.
The key to understanding isoelectric point is to understand how to find what the charge is at any pH, including when the net charge is zero.
To calculate amino acid charge we must take into account the backbone amino group, backbone carboxyl group, and potential acid/base side chain or variable group. (see them all here)
 Let’s start with the simplest amino acid, glycine. With just a hydrogen in place of its variable group, we only have the backbone to examine.
Let’s start with the simplest amino acid, glycine. With just a hydrogen in place of its variable group, we only have the backbone to examine.
As we analyze the structure of glycine at different pH levels, we see only two values, one each for carboxyl and amino groups, on the amino acid pKa table.
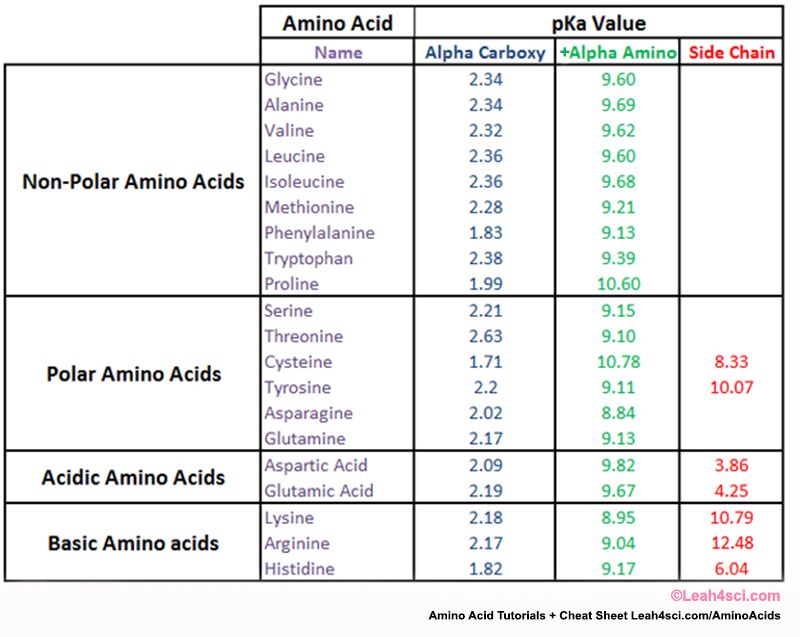
Since pKa relates to an equilibrium constant, you will always have one more structure than the number of pKa values; for example, if there were two pka values, we would expect three structures.
pKa 1 represents the carboxyl group and pKa2 represents the protonated amine group.

When the pH is considerably lower than the pKa we expect both sides to be fully protonated.
There will be no charge at the carboxy, and a positive charge at the nitrogen for a net charge of +1.
When we raise the pH a few units above the first pKa, and still well below the second pKa value, the carboxyl group will lose its proton; however, the amino group is still protonated. This is the zwitterion form, with a positive and negative to cancel out.
When you raise the pH to well above the amino value, the nitrogen will lose its proton and thus its charge. We now have negative and zero for a net charge of -1.
The zwitterion form can exist anywhere between the the 2 pKa values. So how does this relate to the isoelectric point? Do we randomly pick a value?
The answer is no, but let’s take a closer look at the pKa values first.
As explained in the buffer video above , when the pH is exactly at the pKa value, we have an ideal buffer where the molecules exist in equilibrium. For example, if pH = 2.34, which is the pKa of the carboxyl group, what is the net charge?
Since this is the carboxyl buffer zone, we’ll have 50% neutral molecules where the carboxyl is deprotonated, and 50% positive molecules where the carboxyl is protonated.
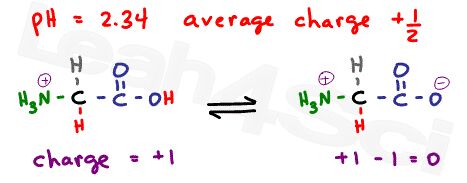
Now if we raise the pH to 9.60, the pKa of the protonated amino group, we get yet another buffer.This time there is an equilibrium between the protonated neutral zwitterion and the deprotonated negative molecule; once again in a 50/50 ratio.
So if each pKa value gives us a 50% neutral molecule, and the isoelectric point is the pH of exact neutrality, we need to go EXACTLY halfway between the two values that give us 50% neutral. The first value gives us 50% neutral and 50% +1. The second value gives us 50% neutral and 50% -1.
The isoelectric point is the average of the 2 pKa values that have a neutral molecule as one of its equilibrium species.
In other words, find the pKa that takes the amino acid from neutral to -1 (9.60 for glycine),
find the pKa value that takes the amino acid from neutral to +1 (2.34 for glycine), and then find the halfway point or average.
pI = (pKa 1 + pKa 2) / 2
Now let’s try it without the drawing, in case you need quick answers from a table on your MCAT.
Given: 2.34 and 9.60, let’s find the average MCAT Style NO Calculator
- Round 2.34 down to 2, round 9.60 up to 10
- 2 + 10 = 12 / 2 = 6
On Calculator 2.34 + 9.60 = 11.94 / 2 = 5.97
On the MCAT, close enough is good enough, and this is pretty darn close.

This sounds like a great deal of work for an amino acid with just 2 side chains. But if you can understand the logic for a simple structure, you’ll be able to apply it to something more complex.
This is especially critical when dealing with acidic or basic amino acids that have a third pKa value for their side chain.
Do we take the average of all three? If just two, which two?
Isoelectric Point for Acidic and Basic Amino Acids
This is where understanding the pI logic comes in handy.
Find the pKa which represents the equilibrium between the positive and neutral form.
Find the pKa which represents the equilibrium between the negative and neutral form.
And average those two.
Let’s try an example for an acidic and basic amino acid:

pI for Glutamic Acid
Looking at the pKa table above we get:
Carboxyl pKa = 2.19
(on the MCAT you can estimate the carboxyl pKa to 2)
+Amino pKa = 9.67
(on the MCAT you can estimate the +amino to 10)
Side chain pKa = 4.25
 Let’s start at a pH of 1. Since 1 is less than every given pKa, we have too many protons in solution and EVERY potential group will be protonated.
Let’s start at a pH of 1. Since 1 is less than every given pKa, we have too many protons in solution and EVERY potential group will be protonated.
That’s neutral for each carboxy, positive for the amino for a net charge of +1. This pKa should automatically pop out at you as the pKa between zero and positive 1. This pKa represents the equilibrium between the protonated +1 and the deprotonated zero.
 Now raise the pH to 3.3, which is almost halfway between the 2 carboxylic acid pKa values. There will be a 10:1 buffering effect happening at each carboxy, given that we’re within 1 pH unit of the pKa value, but we’ll focus on the majority here.
Now raise the pH to 3.3, which is almost halfway between the 2 carboxylic acid pKa values. There will be a 10:1 buffering effect happening at each carboxy, given that we’re within 1 pH unit of the pKa value, but we’ll focus on the majority here.
The most acidic carboxyl will be deprotonated and negatively charged, the less acidic carboxyl remains protonated and thus neutral. The pH is still too acidic for the amino group, which remains protonated and positive. This gives us a net charge of 0 and our zwitterion form.
This pKa represents the equilibrium between the side chain protonated neutral carboxyl and the deprotonated net negative form. We can stop here to find the pKa but let’s continue for the sake of completing this thought.
Remember, 3 pKa values implies 4 structures.
 Let’s raise the pH above the carboxyl value but still below the amino value at a random value of 6.5.
Let’s raise the pH above the carboxyl value but still below the amino value at a random value of 6.5.
6.5 is more basic when compared to both carboxyl pKa values, resulting in both groups deprotonating but still more acidic when compared to the basic 9.67 pKa value of the + amine group. This results in a net charge of -1.
 Now if we raise the pH well above the highest pKa value to a pH of 12, the solution will be too basic for any protons to remain. With so much OH- in the solution, every possible acidic proton will be grabbed off the amino acid and will react with OH- to form water.
Now if we raise the pH well above the highest pKa value to a pH of 12, the solution will be too basic for any protons to remain. With so much OH- in the solution, every possible acidic proton will be grabbed off the amino acid and will react with OH- to form water.
This leaves us with 2 deprotonated carboxyl groups at -2, and a deprotonated and now neutral nitrogen for a net charge of negative 2.
Since the final pKa value represented the equilibrium between -1 and -2, it is not used for pI calculations since pI looks at the pKa values near zero and +/- 1.
So what is the pI value here?
We average the 2 pKa values which have zero charge in their equilibrium.
- pKa of 2.19 represents the equilibrium between +1 and zero
- pKa of 4.35 represents the equilibrium between – 1 and zero
Let’s find the average MCAT style.
Remember, the MCAT is NOT testing your math ability, instead it’s testing your ability to get an answer close enough.
Le's solve this:
- 2.19 rounds down to 2.
- 4.35 rounds down to 4. But keep in mind, if we round down for BOTH values we have to round our answer UP.
- 2 + 4 = 6 / 2 = 3 which means the pI > 3.
On a calculator 2.19 + 4.25 = 3.22 which is CLOSE ENOUGH.
pI for Arginine
Now let’s look at arginine, a basic amino acid.
From the pKa table we get the following values:
carboxyl pKa = 2.17
+amino pKa = 9.04
Side chain pKa = 12.48
3 pKa values, 4 structures
 Let’s start with a pH of 1. Since this pH is below any given pKa value, we have an abundance of protons in solution for a fully protonated amino acids. This gives us a neutral protonated carboxyl, and two positive protonated nitrogen atoms for a net charge of +2.
Let’s start with a pH of 1. Since this pH is below any given pKa value, we have an abundance of protons in solution for a fully protonated amino acids. This gives us a neutral protonated carboxyl, and two positive protonated nitrogen atoms for a net charge of +2.
Clearly this pKa value cannot be used for pI calculation since the equilibrium is between +2 and +1, rather than zero with +/- 1.
 Let’s raise the pH to a neutral 7, which is below both nitrogen values but well above the carboxyl value.
Let’s raise the pH to a neutral 7, which is below both nitrogen values but well above the carboxyl value.
This results in a negative deprotonated carboxylate and two positive protonated nitrogen atoms for a net charge of +1.
 When we raise the pH to 11, we’re now above both backbone pKa values, resulting in a deprotonated negative carboxylate and a deprotonated neutral nitrogen.
When we raise the pH to 11, we’re now above both backbone pKa values, resulting in a deprotonated negative carboxylate and a deprotonated neutral nitrogen.
However, since the pH is still more acidic compared to the side chain pKa value, we have a protonated positive side chain for a net charge of zero, the unexpected zwitterion net zero form.
O nce we raise the pH to 14, which is more basic when compared to any of the pKa values, we get a full deprotonated molecule with a negative carboxylate and 2 neutral nitrogen atoms for a net charge of -1.
nce we raise the pH to 14, which is more basic when compared to any of the pKa values, we get a full deprotonated molecule with a negative carboxylate and 2 neutral nitrogen atoms for a net charge of -1.
Now ask yourself, which 2 pKa values had zero in its equilibrium?
Given a basic side chain, it was the 2 upper pKa values.
pKa of 12.48 represents the equilibrium between neutral and -1
pKa of 9.04 represents the equilibrium between neutral and +1
So we use these to values to find the pI.
- 9.04 rounds down to 9
- 12.48 rounds down to 12. We rounded down for both so we’ll have to round our answer up ever so slightly.
- 9 + 12 = 21 / 2 = 10.5
On a calculator 9.04 + 12.48 = 21.52 / 2 = 10.76 = close enough.
In Conclusion:
Amino acids can exist as zwitterions containing a protonated amine group and deprotonated carboxyl group. The pI, or isoelectric point, corresponding to the zwitterion form lets you calculate the pH at which an amino acid will have a net zero charge. This next zero charge or isoelectric point comes from the average of the 2 pKa values that allow the amino acid to exist in equilibrium between the neutral and positive or negative form.



Thank you for clarifying my doubts regarding charge of amino acids at different pH.
Very helpful explanation and examples, thank you!
If there are 3 pKa values.. Why usually we take the same group or the one with small different pKa value.. I still can’t understand
thank you for the lesson,
However i am really confused about the basicity of the basic amino acids.
I was wondering why histidine < lysine < arginine are in this order of increasing basicity, if histidine has a more stable conjugate acid (protonated form) due to resonance?
pls HOW COULD WE FIND THE ISOELECTRIC POINT OF THE DIPEPTIDE Lys-Lys giving the fact that the zwitterion form of the dipeptide NEVER comes out? thank you in advance
Hi Leah, I have a question regarding protonation states of a protein. When there are a bunch of amino acids in a protein, can the backbone atoms get protonated? (besides the C-terminus, N-terminus and side chains.)
This was the best explanation I’ve come across! Thank you so much for being so thorough.
Hi Leah, great website and tutorials on every subject, very helpful.
Just one question, do AA sidechains from Serine and Threonine not get deprotonated at high pH?
Thank you.
Thank you so much! now I understand it, I didn’t understand it conceptually. I thought I understood it but when it came to the question I would always get confused. THANKS ALOT!
Terrific article. Time saving and clear. Not overly simplified but clear of details beyond the scope of the exam, thank you for your hard work.
Simply the students overlap without knowing how pl value calculated
The way of presenting like that, made it easy to understand
So thank you for your gathered information
Why the amino acids or proteins didn’t precipitate at physiological PH
Thanks for this very helpful
Thank you very much! A few quick Qs. I understand the logic you laid out. However, I don’t understand why the different pHs were chosen; I know they are not, but they seem to be arbitrary to me. It’s a lack of my understanding. Wouldn’t you add up all the pKa 1 + pKa 2 + pKa 3 and then divide by 3 to get the average, which is pI? How could you use this info to relate to an MCAT question about PCR etc? Or how could the pI be used? I watched all your videos on a.a.s and made flash cards. Just a few quick examples and thoughts of yours would be fantastic! Thank you!!
Thanks a lot!!!……I was having a lot of trouble with this topic as to how to find out the pi for amino acids with a side chain group which can be acidic or basic…after reading through this portion I have cleared off my doubts….
Hello Leah, I’m getting to grips with ascorbic acid which has two pKa values (4.17 and 11.6) and thus zwitterionic value of 7.935. I’m attempting to titrate with sodium carbonate and want to predict the titration but do not know how to apply the henderson hasselbalch equation in this case. Perhaps I missed something, sorry. Do I just use the pI in place of one of the other pKa (that seems wrong) or is it impossible to use the H-H equation for zwitterions?
Also, separately, once I have titrated to the pH values I need (need several tightly scatter around neutral but held in position by a buffer) am I right to titrate with sodium carbonate then add PBS or should I be using only PBS to titrate? Thank you.
Can you pl explain about Histidine case with different ph and net charge on it.
This really helps me a lot.. Thanks for clearing my concept and make it firm.
You’re welcome, Pritesh!
Really the article was amazing and very helpful.. It made my concept of isoelectric point crystal clear. I must say the teachers should teach like this way in the classes so that the students can easily understand without a bit of confusion.. You are doing a great job. Thank You.
Thanks Bodhisatwa! Glad you found it helpful! Since teachers won’t all suddenly change, be sure to share this with your classmates
Thank you very much, it was helpful and detailed
You’re very welcome Ahmad
Thanks so much for this series on Amino Acids! I have a question – once we understand the methods shown above for finding pI, can we just say that once we find a case where above or below a given pKa leaves either +/- 2 charge on the amino acid, then we could just find the average of the remaining pKa’s? You need 2 pKa values to take the average of, and if you can eliminate one of the three pKa’s, then you know what’s left to average. Is there ever an exception to that case? I hope that question made sense. Thanks!
I’m not sure I understand what you’re getting at. If there are 3 pKa values take the 2 closer ones and average them as a ‘shortcut’
It doesnt always work. For example Pk values for Tyrosine, Tyr are 2.20, 9.21, and 10.46 but the pI is 5.65. What is the reason for this?
This is Emilio from Spain. I was lost until I found you Leah4sci.
Thank you so much
Muchas Gracias! Glad to help
do we have to memorize the pka values of th aa
I don’t recommend it. Have a general understanding of carboxyl and amino side chain values, acids and bases, and Histidine which is the oddball at around 6.
This is the best article ever! It explains everything in detail with examples and videos. It never gets better than that! Thank you Leah4sci.com
Thank you so much for the kind words Malek. Remember the deep questions you asked on live workshops I know that you’re a thinker and so your comment really made my evening.