 Below is the transcript of my tutorial video on MCAT Physics Video 7 – Free Fall in Translational Motion
Below is the transcript of my tutorial video on MCAT Physics Video 7 – Free Fall in Translational Motion
(Click Here to watch on YouTube)
[Start of Transcript]
Leah here from leah4ci.com/MCAT and in this video we’ll talk about Free Fall as it’ll show up on your MCAT in a Kinematics question.
Free fall as the name implies is when something falls under its own acceleration, meaning you don’t have an outside force that causes it to accelerate in any direction other than straight down. When dealing with Free Fall, we use the standard Kinematic equations.
But realize that anytime X shows up, you want to use Y and anytime Accelerations (a) shows up, you want to use the acceleration of gravity or simply g for gravity. Gravity’s 9.8m/s2 but on the MCAT you can simplify and we’ll use 10 meters per second squared (10m/s^2) with the negative (-) to imply that the direction is downward.
The three equations to consider for Free Fall have acceleration in them. The first is V final is equal to V initial plus at (Vf=Vi + at). We wanna swap out the a for g and since gravity is down, we change gt plus to minus because negative implies a negative or downward direction.
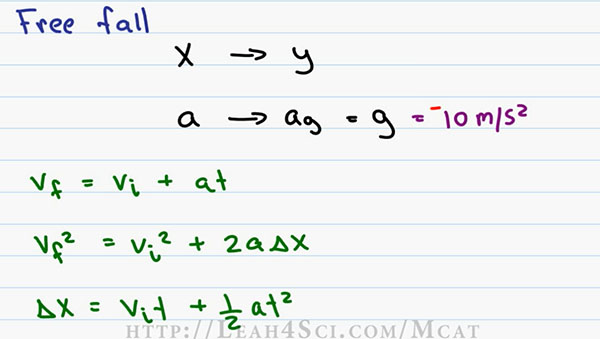
The second one is V final squared is equal to V initial squared plus two a delta X. We wanna swap the X for a Y, a for g and then put a negative for the direction of gravity. And finally the last one is delta x is equal to V intial t plus one over two a t squared. We switch the x to a y , we put negative and swap the a for a g.
Free Fall questions will show up in one or two ways. You can have something falling downwards and then your Velocity and Acceleration of Gravity or both from the same direction. Or you can have something being thrown upward. The initial Velocity for something thrown up is positive but the gravity which is slowing it down and the downward direction is going to be negative.
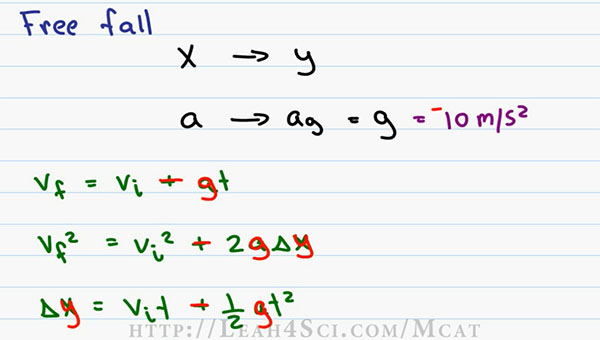
And one thing to keep in mind, because Velocity and Gravity are working against each other, V final which is going to be V at the top is equal to zero. So picture this, you throw something up with the initial velocity and then as it’s going higher and higher gravity is going to push it down and down. So the speed of which the object is going upward is gonna slow down slow down and it’ll comes to a complete stop and then it will change direction and the Velocity will be downward in addition to the Gravity so it will go from no speed at the top going faster, faster and faster until it hits the ground.
We’ll look at this in a more detail when we talk about Projectile Motion but now let’s try a simple free fall problem. In this problem, we’re told that:
A rock is thrown upward and reaches a height of 6 meters. How long does it take for the rock to reach its maximum height?
The first thing we need to do is to identify what we’re given and what we’re ask for. In this case it appears that we’re given only one unit but if you’ll read the question carefully, we’re given two. We’re told that the rock reaches the height of 6 meters that means delta y is equals to positive six meters.

We’re asked for how long it takes to reach the maximum height and that means time is our unknown. But to solve an equation in Kinematics you need to have two given and one unknown. The hidden given in this case is the acceleration which is equal to gravity of negative ten meters per second squared (-10m/s^2).
Ideally we want to use the Kinematic equation that has delta y, t and g. But the equation that meets this criteria is X is equal to V initial T plus one over two a t squared. We swap the X for a Y, turn the a into a g and put a negative sign to imply the direction of gravity.
When a rock is thrown upward, it has the initial Velocity. The problem here is that the initial velocity is not zero and we cannot cancel out this term. If we’re solving for time, we have time showing up as t and as t squared and if we set this up correctly, we wind up with a quadratic equation.
This is not your Physics class, this is the MCAT, you don’t have a calculator and you cannot solve a quadratic. If you’re serious trying to do quadratic, find another way to do it because it’s gonna take too long.
What we want to do here is see if we can solve for another unit within a different kinematic equation so that even though we have to take an extra step it’s still easy and doable in the MCAT. So here’s what we know, looking at the kinematic equations, we know that we can’t use this one cause we have a quadratic, so we want to solve for time using a different equation.
The other equation that relates Gravity and Time is V final equals V initial minus g t. This has time unit in it but also ask for V final and V initial which we don’t have. So the other way to do this is to take on the third equation which is time independent, use that to solve for our unknown variable of Velocity and then go back to this equation and solve for time.
Starting with the equation, V final squared equals V initial squared minus two g delta y (Vf^2 = Vi – 2g∆y). We know that V final or the velocity at the top is going to be Zero because when you throw the rock up it will slow down, slow down and come to a stop. We drop it out the equation.
We wanna solve for V initial so we move that to the other side and this gives us a new equation as follows; Negative V initial squared is equal to negative two g delta y (-Vi= -2g∆y). We have negative on both sides so we can cancel it out and that means V initial squared equals two g delta y. And then all we have to do is plug in and solve.

We have 2 times g which is 10 meters per second squared and delta y which is 6. I like to multiply the numbers that don’t have the ten in it first because multiplying by ten is the easier step. Two times six is twelve, twelve times ten, we just add the zero that’s a hundred and twenty. And if V initial squared is equal to a hundred and twenty, we take the square root of both sides to get V initial.
One hundred and twenty is very close to one hundred twenty one and the square root of one twenty one is eleven so let’s say that this is equal to eleven. If you’re not confident with your square root values, grab my Math Cheat Sheet that has a lot of technique, equations for you to memorize for the MCAT and you can find this on my website at https://leah4sci.com/MCATMATH.
Now that we know that eleven meters per second upward so it’s positive is equal to our V initial, we can now use this value to plug in to the next equation.

The next equation we said we’ll use is V final is equal to V initial plus a t or minus gt (Vf= Vi – gt). We want to solve for time but first let’s get rid of what we don’t need and then isolate t. V final is zero at the top so we get rid of it. To isolate t, we first subtract V initial, that gives us negative V initial is equal to negative gt.
Time cannot be a negative unit and we prove that here by canceling out the negatives on both sides. Now we’ll divide by gravity to isolate t and that gives us V initial over g is equal to t. Our V initial’s eleven meters per second, gravity is ten seconds per meter squared. Realized we’re not using the negative because we’ve already accounted for that in the initial setup of the equation we’re left with just the positive numbers.
Now we have eleven over ten, we’ll use the factor of ten trick. When dividing by ten, it has one zero so we move the decimal back one space and time is equals to one point one second. How do we get second? Meters cancel out, Second cancel out one of the seconds in seconds squared and that leaves us with one over one over second. So the inverse of one over second is second and that’s my answer.
Now I realize this was a little bit of a long winded way to solve for the problem, so to check yourself, you can plug in the numbers and see if that makes any sense. Let’s plug in what we have for here and see if we got an answer for y. we said that V initial is eleven and time was one point one second, we’re obviously gonna round with this to do it quickly and then we’re subtracting one over two, gravity is ten and one second squared is just one squared or one.

I have times ten times one is five. So we have eleven minus five which is equal to six and lone behold our height was six meters.
Be sure to join me in the next video where I take you through Projectile Motion and the way you want to approach it on the MCAT. You can find my entire series on Translational Motion by visiting my website https://leah4sci.com/MCATPHYSICS.
Are you stuck on a specific MCAT topic? I offer Private Online Tutoring where I focus on your needs to strengthen your individual weaknesses. Tutoring details can be found using the link below or by visiting my website leah4sci.com/MCATTutor.
Are you overwhelmed by the sheer volume of information required for the MCAT? Are you worried that lack of a proper study plan and low MCAT score will prevent you from getting into Medical School? My new eBook The MCAT Exam Strategy is 6-Week Guide to Crushing the MCAT will help you formulate a concrete study plan by helping you figure out where you stand now, identify your goals and figure out what it takes to reach them and it’s yours FREE when you sign up for my email newsletter at McatExamStrategy.com. By signing up for my email newsletter, you’ll also be the first to know when I have new videos, MCAT Study Guide Cheat Sheets, Tips and so much more! The link again McatExamStrategy.com
[End Transcript]
Watch The Video Here: Free Fall in Translational Motion


Leave a Reply