 Below is the transcript of my tutorial video MCAT Math Video 5 – Squares and Square Roots in MCAT Style Questions .
Below is the transcript of my tutorial video MCAT Math Video 5 – Squares and Square Roots in MCAT Style Questions .
(Click Here to watch on YouTube)
[Start Transcript]
Leah here from Leah4sci.com/MCAT and in this video, I’ll show you how to solve Squares and Square Roots on the MCAT without a calculator.
When it comes to simple Math like Multiplication and Division, it’s easy to find shortcuts but it’s also easy to fall back on the long form Multiplication and the long Division. When it comes to Squares and Square Roots, it’s even more important to know and understand the shortcuts because you’ll have nothing to fall back on when you’re not allowed to use your calculator.
One of my MCAT students brought up this question in a recent tutoring session.
Find the hydronium ion concentration in 0.05 molar solution of acetic acid given an acid dissociation constant of one point eight times ten to the minus five (1.8×10^-5).
I will discuss this concept in my MCAT Chemistry videos at https://leah4sci.com/MCATChemistry, but for now, let’s focus on the Math. We have a zero point zero five (0.05) molar solution and a ka of one point eight times ten to the minus five (1.8×10^-5).

We’ll set up the equation using the Chemistry trick of ka is equal to x squared divided by the Initial Molarity (ka=X²/Mi) with H+ concentration is equal to X. I like to simplify my equations by isolating X and then plugging in the numbers to solve. So we’ll multiply both sides by the Initial Molarity (Mi) and then take the Square Root of each side to isolate X.
This gives me an equation as follows; X is equal to the Square Root of Initial Molarity which is point o’five (.05) and a ka of one point eight times ten to the minus five, and this is where my students froze. We have a square root and we have scientific notation so how do you proceed?
I’m assuming that you’ve already watched my video on how to multiply scientific notation, if you haven’t you can find it on my website at https://leah4sci.com/MCATMATH.
Starting with Multiplication, we have one point five times one point eight times ten to the minus five (0.05 x 1.8 x 10^-5), this can appear daunting but don’t let it scare you. Remember the trick of times 10 divided by 10 that keeps the overall value the same? That’s exactly how we are going to simplify this. And here’s how we’re gonna do it.
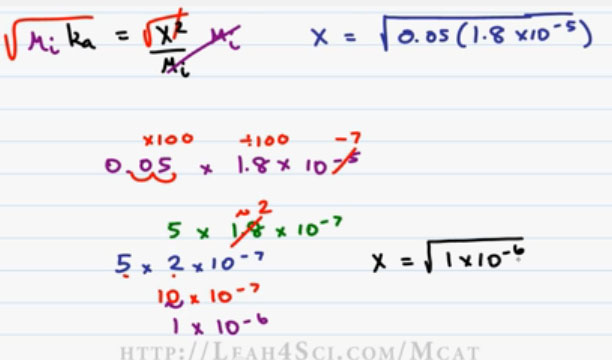
To get rid of the decimal from 0.05, we have to move the decimal two spaces to the right which means we are multiplying by a hundred (100). To make up for it and keep the overall value the same, we do the same thing to the number on the left but in reverse! We’ll DIVIDE by 100; the way we divide by factors of 10 is dropping the exponent 1 value for every factor of 10.
So if I have 10 to the minus of 5 and I wanna make that smaller by a factor of a hundred, 10 to the minus 5 becomes 10 to the minus 6 (10^-6), for ten and ten to the minus seven (10^-7) for one hundred (100) because the difference here is one times ten to the second (1 x 10^2) which is a hundred. This gives me a new number to work with, five times one point eight times ten to the minus seven (5 x 1.8 x 10^-7), much easier to deal with but we can simplify this further.
1.8 is approximately 2 giving me a new value to calculate five times two times ten to the minus seven (5 x 2 x 10^-7). Well 5×2 is 10, the scientific notation we want 1 number and a decimal. So once again we’ll do times 10 divided by 10. Ten divided by ten gives me one (10/10=1), Ten to the minus seven times ten, we move one decimal to the right or raised the power by one so negative seven goes up to negative six giving me an answer of one times ten to the minus six (1×10^-6).
Now going back to the original question, we have x is equal to 1 times ten to the minus 6. We wanna take the square root of the number and the square root of the power and put it together. The square root of one is one so that’s easy. The square root of the power means you simply divide it by two if it’s an even number. The square root of 10 to the minus six is simply six divided by two is three which means one times ten to the minus three (1×10^-3) and that is equal to our Hydronium or H3O+ concentration.
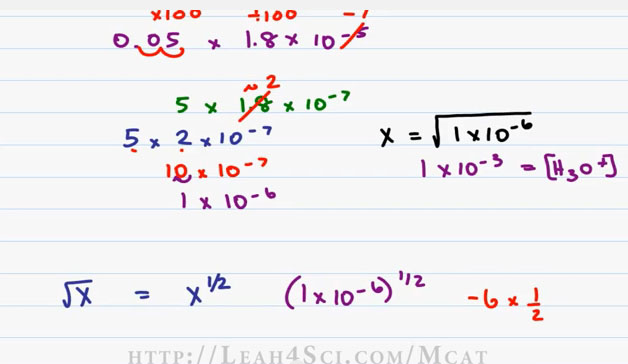
Another way that you can do this is to think about what you know of the Square Root. If you are given the square root of X, that’s the same thing as raising X to the half power (x^1/2). If we apply this to our number we have one times ten to the minus six raising it to the half power (1×10^-6) ^1/2.
When your exponent is raised to another exponent, all you do is multiply the exponents. So here we have negative six as our first exponent times one over two which is our second exponent (-6×1/2). Negative six over two is negative six divided by two and that ones again gives us negative 3 (-3) which is our answer one times ten to the minus three (1×10^-3).
Let’s apply this to another example, say you’re told;
Find the maximum height a feather can reach f it takes off the ground with an initial velocity of 9.3 x 10^-4 m/s. Ignore air resistance.
I’ll go through the Kinematics portion of this question in my Physics series at leah4sci.com/MCATPhysics but for now let’s focus on the Math. The formula we’ll use is V initial squared is equal to V final squared plus 2a delta x (Vi^2 = Vf^2 + 2a ∆x). Since we’re dealing with height and gravitational acceleration, we’ll change the x to a y and positive a becomes negative g for gravitational acceleration.
When an object reaches its Maximum Height the velocity at the top will be zero so we can cross it out. We’re solving for delta y so let’s isolate that by moving everything to the other side. Minus v initial squared gives us a new expression negative v initial squared is equal to negative 2g delta y. Divide by negative 2g on both sides and cancel out the negative for a final expression of delta y is equal v initial squared over 2g (∆Y=Vi^2/2g).
Now let’s plug in the numbers. V initial is nine point three time ten to the minus four (9.3 x 10^-4) so we have nine point three times ten to the minus four squared (9×10^-4)^2, divide that by 2g, the gravitational acceleration is nine point eight meters per second squared (9.8m/s^2) but on the MCAT you’re fine using 10. We’ll skip the units for the sake of focusing just on Math. You have two options here; the denominator is easy, two times ten is twenty but for the numerator we have two options.

Option number 1: We can take that square and distribute it; Option number 2: We can actually write it up as the number times itself. The concept or the ultimate Math to do will be the same so let’s show how to do it by writing it out. We have Nine point three times ten to the minus four times Nine point three times ten to the minus four.
Now remember, on the MCAT you are allowed to round so we’ll round Nine point three down to Nine and then look for an answer that is slightly greater to make up for rounding them. When multiplying the exponents, you multiply the individual numbers so here we have nine times nine which is Eighty One and then we add the exponents. Since both are ten to the minus four we simply add negative four plus negative four giving me negative eight and that will be times ten to the minus eight.
Another option would have been to just distribute the square as follows; if we square nine point three, we have nine times nine which is eighty one, for ten to the minus four square, since we’re taking the power and raising it to a power, we multiply the numbers. Negative four times two is negative eight. So once again we get a simplified version of this number that is Eighty One times Ten to the minus Eight (81 x 10^-8).
So let’s continue, our V initial squared is simplified to Eighty One times Ten to the minus Eight (81 x 10^-8) and we’re dividing that by 20. Assuming that Eighty One is approximately eighty, remember we’re simplifying, when you have two numbers that end in Zero, whatever you do to the top, you can do to the bottom and keep your number constant.
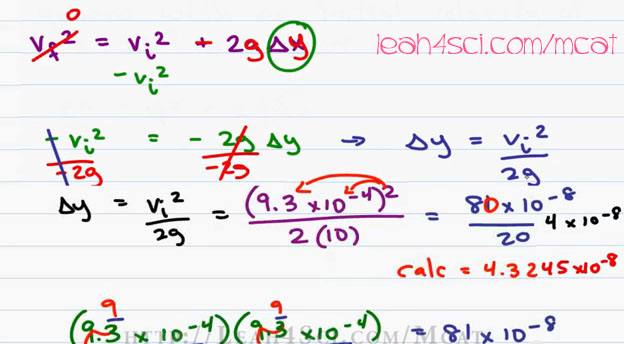
So if I have Eighty over Ten giving me Eight and Twenty over ten giving me Two then I’ve simplified it to Eight over Two. Another way to look at this is you can simply cancel the Zeros. Eight over two is Four so that’ll give me Four times Ten to the minus Eight (4 x 10^-8).
This was a very simplified way of doing the question but look what happened! I punched the initial numbers into the calculator and got an answer of 4.3245×10^-8. Now let me ask you, was it worth saving time to get an answer that is so close even for an MCAT question? Totally!
Be sure to join me on the next video where I break down MCAT Fractions, Percentages and Ratios.
Are you stuck on a specific MCAT topic? I offer Private Online Tutoring where I focus on your needs to strengthen your individual weaknesses. Tutoring details can be found using the link below or by visiting my website leah4sci.com/MCATTutor.
Are you overwhelmed by the sheer volume of information required for the MCAT? Are you worried that lack of a proper study plan and low MCAT score will prevent you from getting into Medical School? My new ebook The MCAT Exam Strategy is 6-Week Guide to Crushing the MCAT will help you formulate a concrete study plan by helping you figure out where you stand now, identify your goals and figure out what it takes to reach them and it’s yours FREE when you sign up for my email newsletter at McatExamStrategy.com. By signing up for my email newsletter, you’ll also be the first to know when I have new videos, MCAT Study Guide Cheat Sheets Tips and so much more! The link again McatExamStrategy.com.
[End Transcript]
Watch The Video Here: Squares and Square Roots in MCAT Style Questions


Hi what would you do if you had an odd exponent, the example showed to take 6/2 to get 3, but what if it were 7 how do I calculate or find the square root of the 7 without a calculator during the MCAT.
Colin: Turn it into an even exponent by multiplication. Your example for square root of 7 is simply an estimation between the square root of 4 and 9. Or did I misunderstand your question?
Your post is really informative sharing the wonderful information about the squares and squares root qith examples. Keep sharing such informative post in future also.
Thank you. Are you a premed student?