 Below is the transcript of my tutorial video Translational Motion Part 3 – Adding and Subtracting Vectors
Below is the transcript of my tutorial video Translational Motion Part 3 – Adding and Subtracting Vectors
(Click here to watch on Youtube)
[Start of Transcript]
Leah here from leah4sci.com/MCAT and in this video, I’ll take you through adding and subtracting Vectors on the MCAT. In the last video we talked about Vectors and Vectors components but an MCAT question may come up with a given more than 1 Vector and you have to put them together.
You can find my entire series on MCAT Physics Translational Motion by visiting my website https://leah4sci.com/MCATPHYSICS. Now this sounds like a very complicated topic, unless you understand what’s going on and understand how to break it up.
A Vector’s simply a line that goes from A to B and if you have more than 1 Vector, imagine that you go from A to B and then you’re travelling from B to C. For example, imagine that this diagram represents a City Grid where we have multiple blocks each at a length of 10 meters.
If I start at point A and walk to point C, I walked a total of 20 meters because I covered the distance of two city block, that’s my one Vector. However, what if I start at Point D, walk for 10 meters and stopped at point E and then walk 10 more meters and stop at point F? What I really did was walk a total distance from D through F for 20 meters.
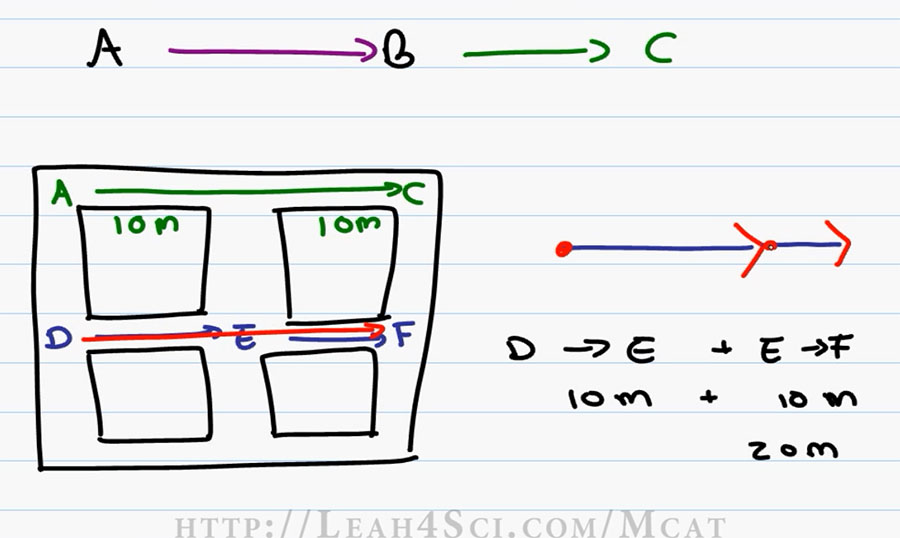
So we took one Vector and we added it to the second Vector to get a total or Resultant Vector. When you’re adding Vectors that are parallel to each other or going in the same direction, you simply add the values. So in the example of going from D through F we had Vector D through E plus Vector E through F, that’s 10 meters plus 10 meters for a total distance of 20 meters.
This is called the head to tail method but students often confused what’s going on. So simply think of the arrow this way: A Vector is simply an arrow, where the tail of the arrow is where you start and the head of the arrow is where you wind up.
If you have one Vector, meaning you stop you have that arrow head and then you start again, it only makes logical sense to start again from where you ended and that’s your new tail and once again when you stop, that’s your new head. That’s the idea of the head to tail method because the second tail immediately follows that first head.
If you see positives and negatives, that can sometimes get confusing. I’ve heard a thought that a positive Vector that you put head to tail but the negative Vector is tail to tail or head to head, I personally find that confusing. Don’t think of your Science as a way to turn your arrow instead, think of it as a direction.
In referring to this grid, we can say that the negative X direction is left. The positive X direction is to the right. Going North that’s the positive Y direction and South is the Negative Y direction.
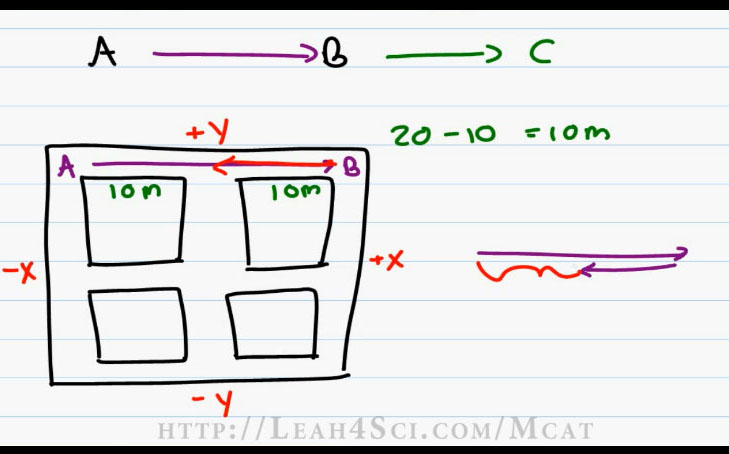
So if I start out at point A and have my first Vector 20 meters to the right at point B and then I stop at point B and change directions going 10 meters to the left, then yes, I wind up having positive 20 because I walked to the right, negative 10 because I walked to the left and that gives me a Resultant Vector of Twenty minus Ten equals ten meters (20-10=10m).
The idea of drawing this head to head to me is personally confusing, so instead, I have my first Vector 20 meters to the right, my second Vector, 10 meters to the left and yes, my Resultant Vector is only 10 meters because I subtracted 10 from my initial twenty.
The same thing happens in the Y direction. If I start out here at point A and then travels negative 20 in the Y direction, meaning 20 meters South, I start with negative 20 and then if I choose to walk 20 meters up, that’s positive 20, positive being the UP direction, and my total displacement is Zero (0) because I ultimately wound up where I started and we can prove this Mathematically because negative twenty plus twenty is equal to Zero (-20 + 20 = 0).
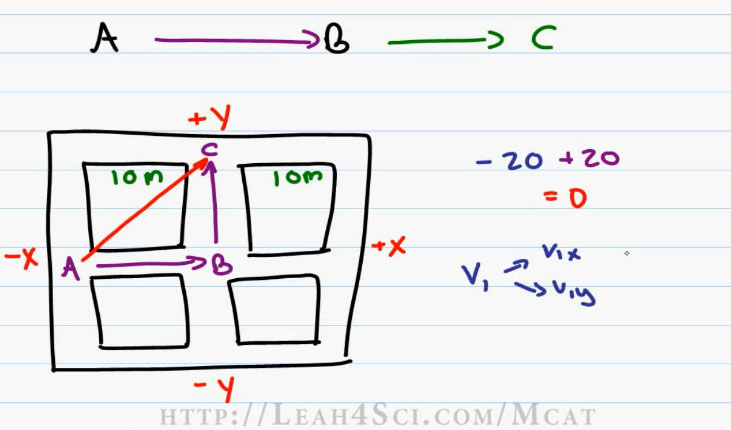
From these examples you can see that if we have Vectors from the same direction we add them, if they’re pointing in opposite direction, you wind up subtracting. So what happens when you start at point A? Walk 10 meters to the right, stop at point B and then walk 10 meters North to stop at point C. What is my total displacement?
I don’t subtract because I’m not walking backwards, I don’t add them because I’m not walking in the same direction. Think of the ultimate displacement on this city grid as the expression as the crow flies. If a crow started out at point A and flew over all the buildings to wind up at point C, the crow is travelling at a diagonal and the total displacement is the exact distance between A to C regardless of the path traveled.
And this is where the idea of Vector Components comes in. if you want to find the Total Distance traveled, you have to take you Vector 1 and turn it into V1x and V1y, then you take your Vector 2 and turn it into V2x and V2y. And then to get the total, we’re going to use the Pythagorean Theorem.
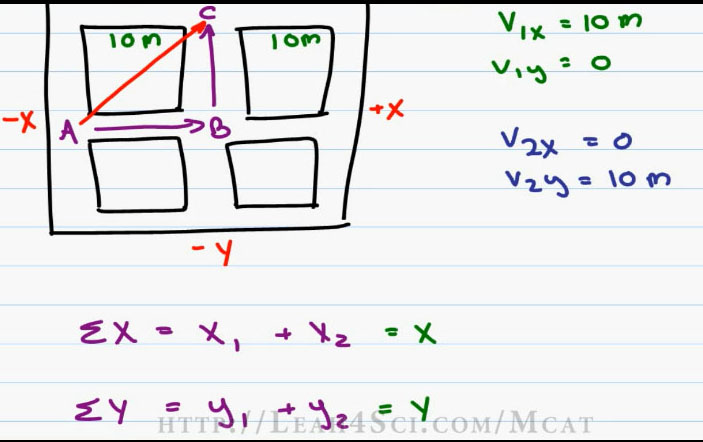
First we have to find the total X so we’ll take the sum of x is equal to X one plus X2 (. The sum of Y is equal to Y one plus Y two (). This will give us our new X and our new Y.
And then we’ll use the Pythagorean Theorem, which is the formula is x squared plus y squared is equal to z squared (X^2 + Y^2 = Z^2). You may also see this as A squared plus B squared is equal to C squared (A^2 + B^2 = C^2). Since we’re solving for C or Z, we take the square root to cancel out the squared and that means the ultimate resultant is simply the square ( ) root of A squared plus B squared or the square root of X squared plus Y squared.
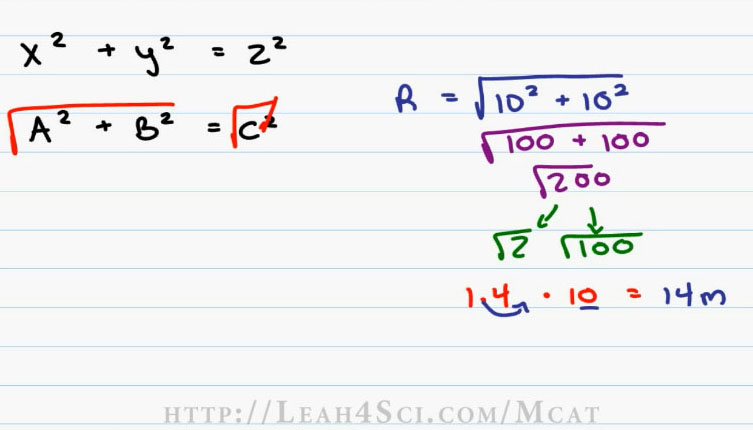
Going back to our example, this is relatively simple because the first Vector V1x is equals to 10 meters (V1x=10m), V1y is equal to Zero (V1y=0) because we’ve only traveled in the x direction. The second Vector we have V2x is equal to zero (V2x=0) because we traveled North so we have nothing in the X direction. The V2y is equals to 10 meters (V2y=10m) because we traveled 10 meters North.
Now be very careful, I’m using V to represent Vector not Velocity. This is just our walking Vector. Adding our Vectors, X1 equals ten, X2 is Zero so X is really just 10 meters. Y1 equals to zero, Y2 is ten, once again we have ten meters.
Plugging our numbers into this equation we have the Resultant is equal to the square root of X squared or ten squared plus Y squared which is ten squared again. Ten squared is a hundred plus a hundred is equal to the square root of two hundred. Remember on the MCAT you cannot use a calculator. So we want to break this up into something that we can recognize.
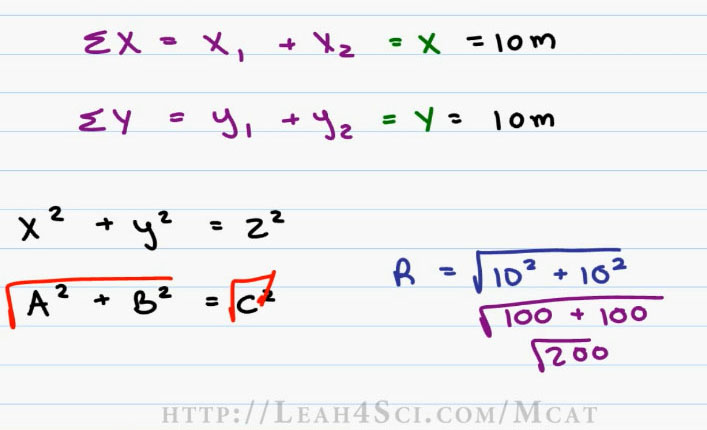
I don’t know the square root of two hundred but the square root of two hundred is equal to the square root of two times the square root of a hundred. The square root of two something you should memorize and that is one point four (1.4), the square root of a hundred is equal to ten (10) and so our answer is one point four times 10 (1.4 x 10). We’ll use the times ten trick moving our decimal over one space to the right and that gives an the answer of fourteen meters total as the crow flies or Resultant of fourteen meters (14m).
If you’re not comfortable with the Math trick I used here, go back to my MCAT Math videos on my website at https://leah4sci.com/MCATMATH. You can also download my MCAT Math Cheat Sheet a lot of the different Mathematical Values that you have to memorize for the MCAT.
Be sure to join me in the next video where I take you through the process of adding vectors that are not clean in the x and y direction making you use Trigonometry to calculate the X and Y components of each Vector before you add them.
Are you stuck on a specific MCAT topic? I offer Private Online Tutoring where I focus on your needs to strengthen your individual weaknesses. Tutoring details can be found using the link below or by visiting my website leah4sci.com/MCATTutor.
Are you overwhelmed by the sheer volume of information required for the MCAT? Are you worried that lack of a proper study plan and low MCAT score will prevent you from getting into Medical School? My new EBook The MCAT Exam Strategy is 6-Week Guide to Crushing the MCAT will help you formulate a concrete study plan by helping you figure out where you stand now, identify your goals and figure out what it takes to reach them and it’s yours FREE when you sign up for my email newsletter at MCATExamStrategy.com. By signing up for my email newsletter, you’ll also be the first to know when I have new videos, MCAT Study Guide Cheat Sheets, Tips and so much more! The link again MCATExamStrategy.com.
[End Transcript]
Watch The Video Here: Translational Motion – Adding and Subtracting Vectors


Leave a Reply