 Below is the transcript of my tutorial video Translational Motion Vectors and Vector Components
Below is the transcript of my tutorial video Translational Motion Vectors and Vector Components
(Click here to watch on Youtube)
Leah here from leah4sci.com/MCAT, and in this video, we’ll talk about Vectors and finding vector components. In part 1 of this series we talked about difference between a Vector and Scaler and said that Vectors have a magnitude and a direction.
But when you’re looking at the direction of a vector, the direction of the vector can be an x-direction, it can be in the Y-direction or it can be in some direction between the x and y axis. If you’re trying to understand and calculate the x and y components of this non-traditional line, you have to know how to break up a vector into its x and y components. For example, you may be faced with a question like this:
A bird takes off from the ground at a 30-degree angle and lands on a tree branch exactly 50 meters away. How far did the bird fly with respect to the ground? How high is the branch?
The bird flew exactly 50 meters, but because the bird flew at an angle, the distance on the ground, meaning if you were to follow under the bird as it flew, would not be 50 meters. Let’s represent this with the diagram. The ground will be our x-axis and the bird takes off at 30 degrees so our angle is 30 for a total distance of 50 meters.

If the bird line on the tree over here, if we’re following along the ground, we would have walk something less than 50 meters and if we want to know the height of the branch that will be significantly less than 50 meters. Now even though this isn’t draw on the scale you can get some idea that the x distance will be closer to 50 than the y. So how do we figure out the x and y components?
We’ll have to use the equation for finding the x and y components of a vector as follows:
If we call the total distance D and we want the x component, then Dx will equal to D cos feda (Dx=D cos and Dy is equal to D sin feda (Dy=D Sin Ɵ). If you’re not comfortable with the related Trigonometry, refer back to my MCAT Math videos which you can find on my website at https://leah4sci.com/MCATMATH along with the Math cheat sheet that shows you the shortcut for what numbers to memorize for different angles.
In this video series, I also show you that Cos we spell with an X (Cosx) and Sin (Syn) we spell with a Y and here you can see, Cos is adjacent because it’s right next to the angle and Syn is opposite because it’s the farthest away from the angle. So let’s see how to solve this without a calculator.
We’ll start by solving for Dx which we set as equal to D Cosx feda (Dx = D cosx and I’m writing the X in there because I want you to get use to recognizing Cos is x for these types of problems. The angle is 30 degrees so we want Cosx of 30. Cosx of 30 is .866 but you should recognize that on the MCAT, we’re perfectly fine using the number point nine (.9). So we’ll rewrite this equation, Dx is equal to D which is our 50 meters times 0.9 which is our estimated cosx 30 value.

The next step again without a calculator is quickly solving for 50 times 0.9 and there are two quick ways that you can do this calculation. The first is to say that 50 times 9 is four hundred and fifty (450) and that’s because five times nine is forty five, we have the zero so that makes it four fifty (450). Point nine (0.9) has the decimal moved one space to the left and so for our answer we move the decimal one space to the left, that gives us forty five meters (45m).
With every answer you want to have the Math solution and the logic solution. Verifying that the answer makes sense, we’ll help you catch careless mistakes if you did the calculations incorrectly. We predicted that the x value will be something close to 50 meters, 45 is very close so we’re good to go.
The second way to solve this is using my factor of Ten trick which I teach on my MCAT Math video three and that’s the idea of times ten divided by ten or moving the decimal. If we have 50 x 0.9, we wanna get rid of the decimal because it’s confusing. We can multiply one number by ten divide the other by ten or simply move one decimal to the right, one to the left. Right, left, new equation is five times nine (5 x 9), this is forty five and I know I’m good to go. That was the x value 45 meters.
Now let’s do the same thing for the Y value. D of Y is equal to D Syn feda (Dy = D syn Ɵ), notice we spell that with the y again. D is 50 meters, Syn of 30 degrees is .5 or one over two (1/2). If your number is clean, I prefer to use a fraction because then I can say that 50 over 2 is 25 rather than try to calculate 50 times point five (50 x.5).
And a good way to recognize this is 25 times 2 is 50 or the value of 2 quarters is 50 cents. If you have half of 2 quarters that’s 1 quarter, that’s 25 cents. Again, we’re just relating the numbers to what we know so that we can quickly solve this without to write out the math in a long and complicated way.
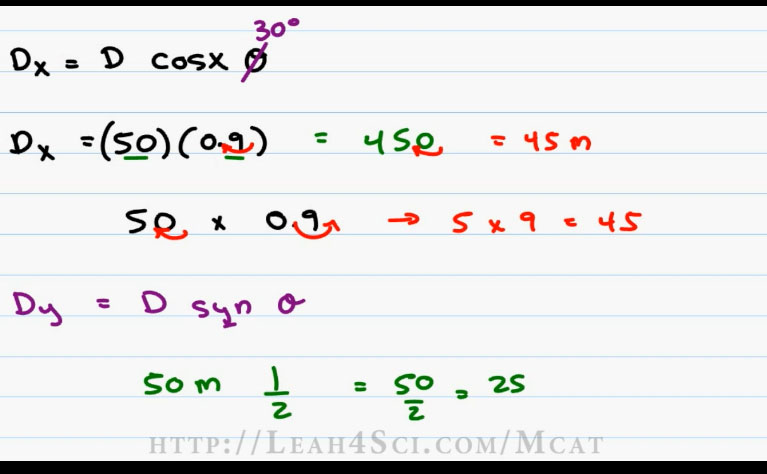
And so for the y value we have 25 meters which is a lot farther from 50 as we initially predicted. After you finish a lengthy calculation, always go back to the question to make sure you answered it correctly. The question asked, how far did the bird fly with respect to the ground, that is our x value, the bird flew 45 meters with respect to the ground. How high is the tree branch, that’s our Y value at 25 meters.
You maybe faced with the question, or you’re given the x or the y component and ask to find the result or ask to find the hypotenuse or the total distance traveled by this object. For example, in this question we have:
A catapult is launched at a 45 degrees angle and travels a total of 4.9m with respect to the ground. Find the total distance.
The numbers we’re given here are 45 degrees, we’re told that it’s 4.9 meters with respect to the ground, so we know that our x value is equal to 4.9 meters. To solve for the total distance, we now have to take the Vector concept but solve for it backwards. On your MCAT, you don’t want to waste time drawing diagrams but I’ll draw on here for the sake of helping you follow along with this equation.
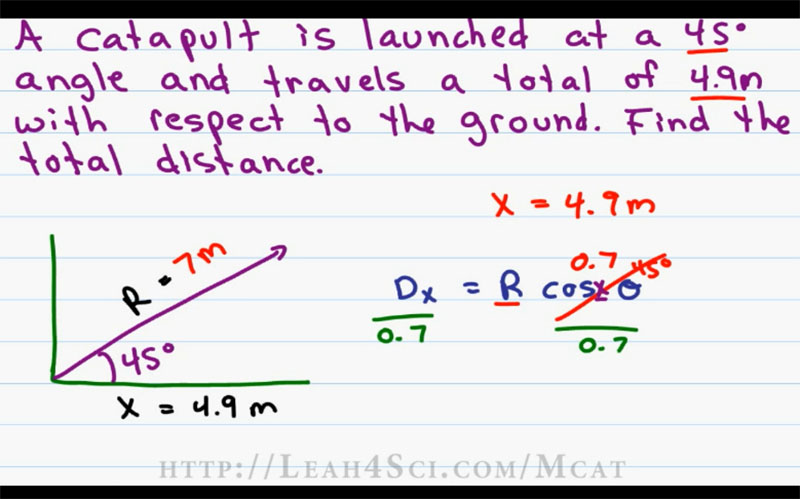
Forty five degrees is somewhere in the middle of ninety so we’ll say that this is our forty five degree angle. We’re also told that the x value is equal to 4.9 meters and the resultant value is unknown. If you think back to how we solve this earlier, the x component, which we’ll call Dx is equal to the resultant or the distance times the cos of the feda value and Cos we spell with an x. We’re not solving for x here, we’re solving for the Resultant.
Let’s replace Cosx of 45 degrees with the value that we memorize, point seven and subtract both sides by point seven to isolate our unknown. Anytime you’re solving for an equation where your unknown is not alone, first, isolate your unknown, rewrite your equation into something simple and doable then start plugging your numbers because you’ll save a lot of time and confusion this way.
And here’s the equation we’re solving for, the Resultant is equal to the distance on the x direction which is 4.9 meters divided by 0.7 which is the cos of 45 value and then we solve. But how do you solve this in the MCAT without a calculator? This is where tricks are really really important.
The first thing I need to do is get rid of my decimals because 4.9 divided by 0.7, in my head it just doesn’t work. There are too many decimals and it’s too confusing. We’ll use the trick of multiplying the top and bottom by ten or simply moving the decimals to the right. If I move the decimals one space for both the numerator and the denominator, I haven’t changed the overall value of this number. If you don’t believe me, punch them both into a calculator and then come back. The number we’re solving for now is 49 divided by 7.

The next thing we want to do is see if we recognize this. 49 divides perfectly by 7 because 7 times 7 is 49. So if we take 7 out of 49 we get 7. We take 7 out of 7 we get 1. Seven over one is simply equal to 7 and that’s our Resultant, seven meters (7m).
Be sure to join me on the next video where I show you how to add Vectors and Vector components, MCAT style.
Are you stuck on a specific MCAT topic? I offer Private Online Tutoring where I focus on your needs to strengthen your individual weaknesses. Tutoring details can be found using the link below or by visiting my website leah4sci.com/MCATTutor.
Are you overwhelmed by the sheer volume of information required for the MCAT? Are you worried that lack of a proper study plan and low MCAT score will prevent you from getting into Medical School? My new ebook The MCAT Exam Strategy a 6-Week Guide to Crushing the MCAT will help you formulate a concrete study plan by helping you figure out where you stand now, identify your goals and figure out what it takes to reach them and it’s yours FREE when you sign up for my email newsletter at https://MCATExamStrategy.com . By signing up for my email newsletter, you’ll also be the first to know when I have new videos, MCAT Study Guide Cheat Sheets Tips and so much more! The link again https://MCATExamStrategy.com.
[End Transcript]
Watch The Video Here: Translational Motion Vectors and Vector Components


Leave a Reply