Below is the written transcript of my YouTube tutorial video MCAT Physics Forces – Equilibrium and Free Body Diagrams Video
If you prefer to watch it, see the video HERE, or catch the entire MCAT Physics Forces series HERE
(click here to see the video on YouTube)
[Start Transcript]
Leah here from leah4sci.com/MCAT and in this video we'll talk about Force Equilibrium and Free Body Diagrams in preparation for the MCAT. Now I teach this topic with caution because free body diagrams can be very time consuming and on MCAT you don't have that time. So instead I'll show you what to do and I want you to utilize this in practice but when it comes to your practice exam and you real exam, I want you to try to simplify this as much as possible so that you don't waste any time.
When we're dealing with equilibrium, you'll often see an object that isn't moving or does not have a net force in any direction. You can call the subject the equilibrium to imply that the forces in the different directions are all equal or they all cancel out. But there are different types of equilibrium to consider. Translational Equilibrium has to do with motion, so that means that if you have an object that has a force in one direction and it won't be moving but then you have a force in the other direction canceling it out that's considered Translational Equilibrium. But, that means the object doesn't have a net force, it necessarily mean that the object is stationary.
Let's use a simple block where the demo force is gravity and the upward force is the normal force. This block is not moving in the Y-direction because it is in equilibrium, meaning the upward force and the downward force perfectly cancel out or simply the sum of the force in the y-direction is equal to zero. But now for example, if the block is moving to the right or the left with constant velocity that means the change in velocity is equal to zero and change of velocity over time is equal to acceleration. So if delta v over t is zero then f equals ma, a is zero, force is zero, this object is still in equilibrium but this is considered dynamic equilibrium, it doesn't have a net force, it still has a constant velocity and is moving. To say that an object is not moving at all, that's when you wanna talk about Static Equilibrium where you have the constant velocity of zero, it's static, it's not moving.
When setting up this equilibrium equations, it helps if you omit those signs. For example the positives and negatives and instead, think of what the sign implies so you have a logical diagram because the signs can confuse you but the logic behind the signs will help you with your drawing. A standard free body diagram is basically taking your object out of the story, out of the question and draw arrows to represent the different forces acting on this object. I like to draw a free body diagram with either a square, a block or a dot and this block can represent anything, from a person to a car to a hammock, any object is easier to draw than a block, than trying to waste time drawing pictures especially if you're not an artist, because this is a Science subject, not art.
Now regardless of the size of this object, unless you're specifically being tested on central mass or central gravity, assume that the entire mass of the object is concentrated in the center of the block or the dot that you're drawing. And that means all the forces can come out of that one object instead of having to figure out where to draw it on a complex item. See this block is resting on a table we'll show that the downward force is the force of gravity or mass times the acceleration of gravity, the upward force is the normal force because the normal force applies to any object resting on a surface. Now let's see the wind is attempting to force to the right. We will draw an arrow to the right and call this force of the wind and you can put whatever subscript you want under the f as long you know what you're referring to. Some of these are common, Fn normal force, Fg gravity but in the last video we were Fp, the force of a person, Fw the force of the wall, as long as you know what you're talking about, you're fine. But now let's say the block isn't moving despite the wind trying to push it, we can show that the force of friction is countering the force of the wind. Now this object here is in equilibrium so all you do is set this equal to each other regardless of positive or negative and let me show you how it works out.
If I tell you that the block has no motion or acceleration on the X-direction, we can assume that the sum of the forces in the x-direction is equal to zero and since the forces are force of friction and when in the opposite direction we can say that the force of friction equals force of the wind. This is without using any positives or negatives, just logically saying if one is to the right and one is to the left they're opposite and therefore they are equal to each other if there is no motion. If you want to get technical you can set it up as sum of the forces in the X-direction equals zero which is equal to positive to the right so that's gonna be force of the wind, negative for the left, force of friction and when you solve it, you'll actually get the same equation we wrote earlier but jumping straight to the setup that doesn't have any signs is faster if you understand how to set this up. Now we can do the same thing for the Y-direction.
We know the block isn't moving so the sum of the forces in the Y-direction are equal to zero, the actual force is force normal and I write Fn so it's not to confuse it with the capital N for Newtons. The upward force is force normal, the downward force is force gravity, they are equal and opposite to each other so we set the equal to each, that's the fast way now let's show it the other way.
If the sum of the force is in the Y-direction is equal to zero, that is equal to the normal force upward, positive minus the gravitational force downward so that's negative and ones again if we re-write this equation we get what we already have. Now imagine we have the same block sitting on a frozen lake that has a low amount of friction so that the force of the wind still cancels the force of friction but there is a net velocity on the object. So let's say there was a strong gust of wind and the object started moving and then friction opposes it just enough to cancel out any acceleration but the block is still moving at a constant velocity. The block is still in translational equilibrium in this case dynamic equilibrium. We can still set up the free body diagram because the sum of force is equals zero even though it's moving at a constant velocity.
Other free body diagrams that you may see is, let's say this block now represents a toy wagon and you have a kit moving it at some angle feda. So that will be your angle feda. If it's being pushed or pulled at an angle the way you set it up is going to be the same, but if the force is now in a slightly upward direction, you're dealing with something between the X and Y components and you want to break it up so you can clearly see what's happening in the X and what's happening in the Y direction. Down still force in gravity, up still the normal force. But now we have an additional component add in the y direction. We take that force either a push or pull at an angle we have to break that up into the force x and the force y using trigonometry and now when you set up the equation you have the sum of the forces in the y-direction is going to be the force applied or the green force positive, the normal force positive and the gravitational force negative and that's still equal to zero because the block is still moving upward down. But now when you setup the x-direction you can say the sum of the forces in the x-direction, let's call this as applied X so F-a-x, is going to be positive F a x which you would set up as F applied cosine of feda and then if you have friction, you'd set that up in the opposite direction. If you don't have friction then you have F of x equals mass times acceleration.
The scary free body diagram for most students is the inclined plane and that's because we're dealing with an object that is not sitting on the x or y axis rather somewhere between. Now I break this down in detail in the Trigonometry video which you can find on my website at leah4sci.com/MCATMath and that's where you see exactly why I'm about to do what I'll do, now I'll just give you the overview. All we do is switch the axis so that X is at angle but parallel to the inclined plane and Y is also an angle but perpendicular to the inclined plane.
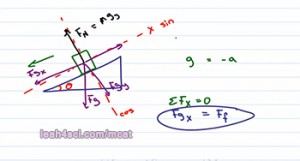
In the Trigonometry video I proved to you why given an angle feda X is going to use Sin rather that Cosine and why we'll use Cosine rather than Sine but everything else is still the same. Gravity does not change just because the incline changes and so gravity go straight down. If gravity go straight down and it's between the X and Y component you have to break it up so that your force of gravity in the X direction is going to be Sine of your angle and force of gravity in the Y-direction is going to be Cosine of the angle. Now we don't care force gravity in the Y-direction, we do care about the normal force which is equal to mass times gravity in the y direction, that's where we care about the cosine component. And if you have friction, that goes in the opposite direction to the X component.
Another confusing factor here is when to use positive and when to use negative. Don't worry about the signs that you're given, turn every sign into something logical. So for example, gravity is a negative acceleration because it goes downward. Don't worry about the negative. Gravity in this case goes to the left. Friction is negative because it opposes the direction of motion. But in this case friction is towards the right so if I try use negative it'll be very confusing. Now if I tell you that this block is not sliding down the incline plane, then I can assume that the sum of forces in the X direction are equal to zero. If the sum of the forces in the X-direction equals to zero then I can say that force of gravity in the X-direction is equal to the force of friction and I don't have to worry about which one is negative or positive because again this is where it gets confusing. Instead, in this case gravity goes to the left because the way the incline plane is drawn goes left. Friction goes to the right so don't worry about your negatives and positives and just set it up this way. If you do have to set up a more complex equation pick one and stick with it, as long as you're consistent it'll work out. I can choose this to be negative and this to be positive making the gravitational acceleration negative but the friction positive and then you typically wanna choose positive y upward and negative y downward, ones again setting those equal to each other.
Notice here that the normal force is mg with a component of gravity so that's mg cosine of feda which perfectly balances the force of gravity downward setting the sum of the forces y equal to zero. Again for the breakdown of why will you sign it cosine opposite to the normal convention, be sure to see the Trigonometry video where I show it in detail. Don't take that explanation as something you have to apply each time but it needs to be intuitive so that you don't waste time being confused on this.
Let's do one more free body diagram. Imagine we have a hammock suspended from two trees, that'll be the hammock and we a student here laying in the shape studying for his MCAT. If you want to calculate the sum of forces here, the first thing you want to do is trend this entire system into one point. If you take the time to draw the hammock on the MCAT you're wasting too much time. Here you have tree 1, tree 2, here we have the student with a hammock as a dot and here we have the ropes that support the hammock. Let's make this bigger so that we can mark it up. Ones again we set about with these sum of the forces. Downward we have force of gravity the student in the hammock. Upward in this case, we have not the normal force but the force of tension in the ropes that support the hammock. We have two ropes sitting at some angle between the x and y component and so we have to break them up into their vectors.
Assuming the ropes are at the same angle, the sum of the forces in the X direction equals zero, coz the hammock isn't moving. That means the tension to the x of one rope equals and balances the tension x in the other rope. We can simply call as positive x and negative x. Assume they cancel out and don't worry about the math. But the tension in the y direction can get tricky. The sum of the forces in the y direction equals zero and you can set it up as force of gravity is equal to two time tension in the y direction. The reason it's two is because half of it goes to one rope and half of it goes to the other rope and obviously you'll find this using the angles given in Trigonometry but don't worry we'll tackle tension by itself in its own video.
You can find my entire series on MCAT Forces along with cheat sheet and practice quiz by visiting my website leah4sci.com/forces.
Are you stuck on a specific MCAT topic? I offer Private Online Tutoring where I focus on your needs to strengthen your individual weaknesses. Tutoring details can be found using the link below or by visiting my website leah4sci.com/MCATTutor.
Are you overwhelmed by the sheer volume of information required for the MCAT? Are you worried that lack of a proper study plan and low MCAT score will prevent you from getting into Medical School? My new eBook The MCAT Exam Strategy A 6-Week Guide to Crushing the MCAT will help you formulate a concrete study plan by helping you figure out where you stand now, identify your goals and figure out what it takes to reach them and it’s yours FREE when you sign up for my email newsletter at McatExamStrategy.com. By signing up for my email newsletter, you’ll also be the first to know when I have new videos, MCAT Study Guide Cheat Sheets, Tips and so much more! The link again MCATExamStrategy.com
[End Transcript]
Click here to Catch my entire video series on MCAT Physics Forces
