Below is the written transcript of my YouTube tutorial video MCAT Physics Forces – Newtons Second Law of Motion Video
If you prefer to watch it, see the video HERE, or catch the entire MCAT Physics Forces series HERE
(click here to see the video on YouTube)
[Start Transcript]
Leah here from leah4sci.com/MCAT and in this video we'll talk about Newton's second law as it applies to your MCAT. You can find my entire video series along with my cheat sheets and practice quiz by visiting my website leah4sci.com/Forces.
When you think of Newton's second law, the equation that should immediately pop into your head is the sum of the forces is equal to mass times acceleration where this symbol here means the sum or simply the addition of . What this tells you is that an object experiencing a net force will experience acceleration in that direction. So what does this mean? In the last video we talk about a block sitting on a table experiencing no acceleration to the right or the left meaning that it's at rest. But we also mention that it's experiencing force of gravity downward. And the force of gravity is mass times the acceleration of gravity or simply mg. What prevents the block from just going straight to the table is another Force in the upward direction completely cancelling out the gravitational force and that's the normal force. And don't worry we'll devote an entire video to just the normal force calculation.
The idea here is that if I set up the equation for the upward and downward force in the Y-direction you'll notice that they completely cancel out and therefore the sum of the force in the up and down direction equals zero, the block does not experience acceleration. But I push the block to the right with a force greater than the opposing force of friction, then the sum of the forces in the x-direction is to the right and the block will experience an acceleration, ones I let go of the block the force of friction is greater than the motion and so the block will to slow down and experience an acceleration to the left because friction is opposing the direction of motion. Again we'll have an entire video just on friction.
For now I just wanna focus on the setup to make sure that you understand what's going on. If you have an object experiencing a force, to calculate the acceleration based on all the different forces, you want to take into account two different versions of this equation. So this is our object in question, we want to look at the sum of forces in the X-direction which is equals to mass times acceleration in the x-direction and to set this up, you want the positive x to be towards the right and negative x to the left. But you must also take into account the sum of the forces in the y-direction which is equal to ma in the y direction. And to set this up you have your upward force as positive y and your downward force as negative y.
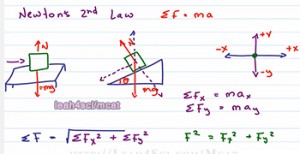
A common scary example where this applies is say I have the same block but instead of the table it's sitting on an incline plane at some angle feda, I can still show my force going down and normal force going up but here's where things change. The force of gravity is still going straight down, that's mg. And the normal force is perpendicular to the surface that object rests on, that's my force end. Now don't worry, I'll do an entire separate video on how to do this type of normal force calculation. What you want to recognize here is that the normal force does not completely cancel out the force of gravity because that's in the y direction but the normal force sits somewhere between x and y direction.
So if I take the normal force and break it down to y components, you'll notice that the y component bouncing gravity is less than gravity because the rest of the normal force is in the x direction and that means gravity will still have an effect on this object and make it move downward. This is where we have the sum of forces favors the x direction and favors the motion of the block sliding down.
Ones you found the sum of the forces in the x direction and some of the forces in the y direction, you can find the total force which maybe in the xoy direction or at some vector in between the two axis. To find the total force you want to set up the equation, the sum of the forces is equal to the square root of the sum of the forces in the x direction squared plus the sum of the forces in the y direction squared and this comes from the Pythagorean Theorem which tells you that F squared is equal to Fx squared plus Fy squared. If you're not comfortable with this, go back to my MCAT Math video series on my website leah4sci.com/MCATMath.
If this sounds overwhelming don't worry. Yes you need to know every step and you need to be able to calculate all the way through but the MCAT questions are likely to give you a setup where you'll intuitively know that one or the other equal zero letting you simply your calculation so that it doesn't take too long.
Be sure to join me in the next video where we talk about Newton's third law. You can find my entire series along with the Forces cheat sheet and practice questions by visiting my website, leah4sci.com/Forces.
[End Transcript]
Click here to Catch my entire video series on MCAT Physics Forces
