 Below is the transcript of my tutorial video MCAT Physics Translational Motion Video – Adding Two Dimensional MCAT Vectors Using Angles and Vector Components
Below is the transcript of my tutorial video MCAT Physics Translational Motion Video – Adding Two Dimensional MCAT Vectors Using Angles and Vector Components
(Click Here to watch on YouTube)
[Start Transcript]
Leah here from leah4sci.com/MCATPHYSICS and in this video we’ll continue our discussion on Adding and Subtracting vectors focusing on Vectors that are given at some angle feda where you have to find the X and Y components.
If you missed the first parts of this video, go find it on my website at https://leah4sci.com/MCATPHYSICS. Let’s start with the simple question to review and then go into angles.
Say you’re asked to find the total displacement if a biker travels 8km east then turns and bikes 6km North. Since the biker is not traveling in one direction you can’t simply add the numbers. Instead you have to take each league of the journey from the X and Y components and then use the Pythagorean Theorem to find the total displacement or the Resultant.
We’ll draw a quick sketch. We have a displacement of 8 kilometers east or to the right, followed by 6 kilometers North. Notice that I have the head to tail method going here. We start at the tail and end at the head, in return we have a brand new tail and end at the second head.
The total Resultant Vector is a line going from the very first tail to the very last head and we call that R for our Resultant. The reason I chose this example is because on the MCAT, in addition to knowing Math equations and how to solve them, you also want to look out for tricks and patterns that will save you time.
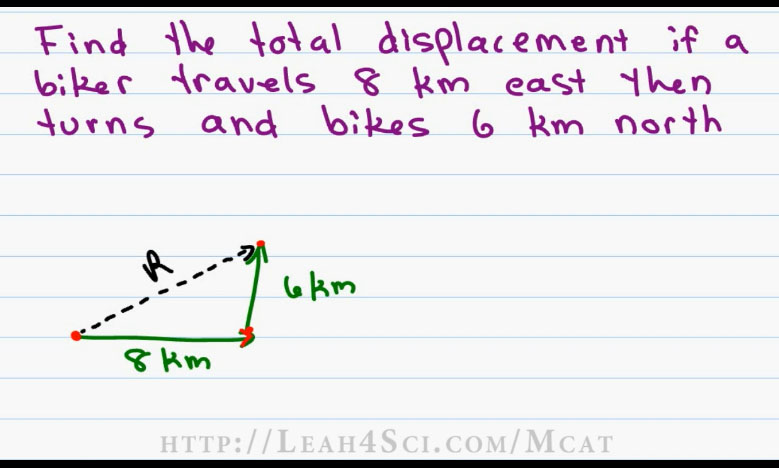
There is a triangle that has the angles 36 to 90 degrees will fall into a pattern of what we call a 3 4 5 triangle. And the 3 4 5 triangles as follows: If you have your short side at a length of 3, your longer side a length of 4, the hypotenuse will be a length of 5. If you can recognize the triangle in your MCAT that has some factor of these numbers, you can save yourself the trouble, save yourself the math and get the answer right there.
Notice that we have 6 and 8. Six is two times three; eight is two times four so we expect the Resultant to be two times five for a total of ten kilometers. Now let’s prove it mathematically.
We’ll use the components B1 for biking the first league of the journey and B2 for biking the second league of the journey. The first league of the journey is 8 kilometers in the x direction so we have B1x is equal to eight (B1x=8). Since B1 is only in one direction, B1y is equal to zero.
The second league of the journey is only in the Y direction so B2x is equal to zero, B2y is equal to six. And so x or the sum of x is equal to eight plus zero which is eight. The sum of Y is equal to six plus zero which is equal to six. And the resultant comes from the formula X squared plus Y squared is equals to Z squared (X^2 + Y^2 = Z^2) or Resultant squared.

Know this formula and be confident enough that you don’t have to write it this way, instead you should simply write the Resultant is equal to the square root of X squared plus Y squared. In this case x squared is eight squared or sixty four, Y squared is six squared or thirty six. If we have sixty four and thirty six, sixty and thirty is ninety, four and six is ten which gives us ninety plus ten or a hundred, that means the resultant is the square root of one hundred which is equal to ten and that’s the number we initially predicted.
If you’re not comfortable with the multiplication that we did here, download my Math Study Guide Cheat Sheet which you can find on my website at https://leah4sci.com/MCATMATH.
Here’s another question that you may find in your MCAT practice material. Now keep in mind the MCAT will not ask you something this tedious and detailed when it comes to Math because they’re testing you in your ability to apply equations and concepts, they’re not looking for you to waste an hour on a single Math calculation. The reason I’m including this is because I want to make sure that you’re comfortable with every single component that shows up within this question so that you’ll know what to do if you’re face something along this line. The question says:
Find the total displacement if a dog runs 59 meters at 45 degrees to the horizontal, then turns North running 31 meters at 30 degrees with respect to the vertical.
This is a little bit of a tricky question so make sure that you break it down and understand what’s going on here. For something like this, it helps if you draw a quick sketch and then work of the sketch rather than trying to pick the numbers out of the story.
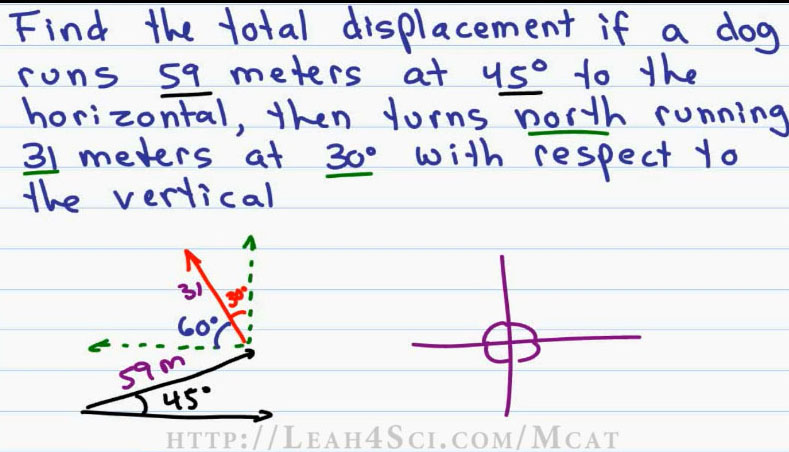
So we have two vectors here, the dog is running 59 meters at 45 degrees to the horizontal. So let’s start with the horizontal and then set the angle at 45 degrees with the vector that is 59 meters long. The second vector is in the Northern direction for 31 meters at a 30-degree angle with respect to the vertical.
This trips off a lot of the students so be careful. If we draw a vertical or a Y component, it helps if you can also see an x component for that new set. It’s almost like we’re putting two different graphs together. If we have 30 degrees with respect to the vertical, that’s 30 degrees from the Y axis and not the X axis. If we draw a 30-degree angle and then start to calculate, we’re looking for everything to fit into a single coordinate system and that means we want all angles to be with respect to a graph that comes out of here.
These are our angles and that means that 30 degrees won’t work, we need to find the angle on the other side of that 30 degrees and that’s why I drew the X and Y components. The angle between X and Y is 90 degrees and so if we have 30 degrees at the top, we do 90 minus 30 and we’re actually looking at the 60 degree angle at our calculations rather than the 30 degree angle.

Since the dog is running, we’ll call our first Vector R1 for run 1, we’ll call the second vector R2 for run 2 and we have to now break down the individual X and Y components. For R1, we have 59 meters at a 45-degree angle. That means R1x is equal to 59 cos 45 and R1y is equal to 59 sin of 45.
The reason I need to use Cos for X and Sin for Y is because I’m referring to my trick of spelling cos with an x and syn with a y. I talked about this trick in my Trigonometry video which you can find on my website at https://leah4sci.com/MCATMATH. In that video I also talked about the shortcut values to memorize for the Sin and Cos values. 45 degrees is going to be the same for Sin and Cos and we’re using the value of 0.7 and so we have 59 times 0.7 for the X and y values.
Calculating this exactly will take too long so we’ll take the shortcut of rounding 59 to 60, that’s very close and multiplying 60 times 0.7. I’ll use the trick of times ten divided by ten or move one decimal to the right and one decimal to the left. Also a topic covered on my Math videos and that means I move this one to the right and this one to the left giving me six times seven which is forty two.
Now moving on to R2. For R2 we have 31 meters at a 60-degree angle and that means R2x is 31 cos with an x of 60 and R2y is equal to 31 syn 60. The value to memorize, cos of 60 is 0.5, syn of 60 is 0.866 but it’s okay if you memorize and use the value of 0.9.

So let’s calculate what we have. Thirty one times point five, that’s approximately thirty times point five, thirty over two which gives me a rounded value of fifteen. And thirty one times point nine, ones again we’ll use the decimal trick move that to the right, move that to the left that gives me three times nine which is twenty seven (3×9=27). That’s equal to X and that’s equal to Y.
Now that we have our Vector components we wanna add them up. So we’ll have the sum of X is equal to X1 plus X2 (εx=X1+X2). The sum of Y is equal to Y1 plus Y2( εY=Y1+Y2). X1 is forty two (42) and X2 is fifteen (15) but be careful about the direction. Notice that R1 goes to the right which is a positive direction, R2 goes to the left which is a negative x direction and so it’s really plus negative 15 or simply minus 15. Forty two minus fifteen is a little hard to do, you can try forty minus fifteen which is twenty five then add back the two giving you twenty seven (27). Y1 is forty two Y2 is twenty seven, forty and twenty is sixty, two and seven is nine giving us a value of sixty nine (69).
And now we solve for the Resultant. The resultant is the square of X squared plus Y squared, in this case the square of twenty seven squared plus sixty nine squared ((R=√(〖27〗^2+〖69〗^2 )) . These numbers are very hard to do the long way so we’re going to round. And since we’re rounding everything up, we’re going to assume that our answer will be slightly less. Remember we’re making our numbers bigger so make sure you compensate by making your answers slightly smaller. We’ll square thirty and seventy.
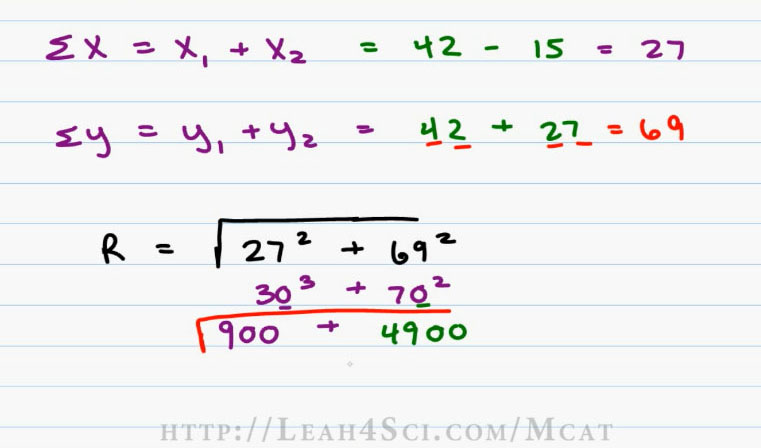
While we don’t know 30 squared I know three squared is nine and then I add two zeros, one for each of the thirty and that gives me nine hundred. I do the same for seventy. Seven squared is forty nine and I add two zeros, one for each seventy that I’m using. Now we add Nine hundred and forty nine hundred. If we look at forty nine as fifty, that’s fifty nine so the answer will be fifty eight and then we have fifty eight hundred (5800).
And finally we take the square root of that. I don’t know the square root of fifty eight hundred but I do know that it’s equal to the square root of fifty eight times the square root of a hundred. The square root of fifty eight is not a number that I know, so I try to find a recognizable square below and above the number that I’m given.
The square root of forty nine is less than the square root of fifty eight which is less than the square root of sixty four. Rad forty nine is seven, rad sixty four is eight. So we’ll guesstimate that our answer is approximately seven point five. The square root of one hundred is ten, that’s simple enough and our final calculation is seven point five times ten. Whenever you multiply by ten we move the decimal to the right which gives us a Resultant of seventy five meters (R=75m).

Keeping in mind that we did a lot of rounding to get to where we are, I punched the initial values into the calculator and got an answer of Seventy three point three (73.3) which given the amount of rounding we did is very very close. Now remember, on the MCAT you will not have this many steps in a single question but you do have to know how to approach this in case you’re faced with a question that is similar to any part of this long question that we just solved.
Be sure to join me in the next video where we start our discussion in Kinematics by talking about speed and velocity as it appears on the MCAT.
Are you stuck on a specific MCAT topic? I offer Private Online Tutoring where I focus on your needs to strengthen your individual weaknesses. Tutoring details can be found using the link below or by visiting my website leah4sci.com/MCATTutor.
Are you overwhelmed by the sheer volume of information required for the MCAT? Are you worried that lack of a proper study plan and low MCAT score will prevent you from getting into Medical School? My new ebook The MCAT Exam Strategy is 6-Week Guide to Crushing the MCAT will help you formulate a concrete study plan by helping you figure out where you stand now, identify your goals and figure out what it takes to reach them and it’s yours FREE when you sign up for my email newsletter at MCATExamStrategy.com. By signing up for my email newsletter, you’ll also be the first to know when I have new videos, MCAT Study Guide Cheat Sheets, Tips and so much more! The link again MCATExamStrategy.com.
[End Transcript]
Watch The Video Here: Translational Motion – Adding and Subtracting Angled Vectors



Leave a Reply