The first step to learning resonance structures in organic chemistry, is to comfortably know the answer to this question:
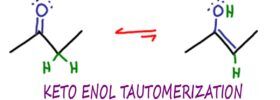
What is Resonance?
Don't just memorize ‘these arrows move here'. Instead, make sure you get why molecules resonate to delocalize their electrons, and understand the difference between ‘resonance hybrid' and ‘resonance intermediates'. This and more is covered in the video below
(Watch on YouTube: Resonance. Click cc on bottom right for video transcription.)
Links & Resources Mentioned In This Video:
–> Watch Next Video: Key Arrow Patterns in Resonance Structures
This is Video 1 in the Resonance Structures Video Series. Click HERE for the entire series.
Ready to test your resonance skills? Try my FREE Resonance Practice Quiz.
When you drew the three structures for NO3-, why don’t we place a double ended arrow between the bottom two structures going from the far right structure to the far left structure (the pi bond going from the far right oxygen atom to the far left oxygen atom)?
You are the best teacher I have ever met
Excellent video!
How can you determine the charges on the oxygens ?
Excellent explanation.God bless you
thanks ma’am
You’re welcome
dear Leah thanks for yours videos they means all the difference for me. you are helping me to understand organic chem.
You are very welcome Ruth. Glad to help