Hydride shifts and methyl shifts can occur in organic chemistry reactions if there is a carbocation intermediate. While Markovnikov’s rule places the carbocation on the more substituted of the 2 former sp2 (double-bound) carbon atoms, if there is an EVEN MORE substituted carbon nearby, you’ll get a carbocation rearrangement. These videos help you understand the […]
Proton Transfer and Rearrangement Mechanisms in Organic Chemistry
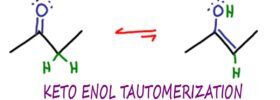
Proton transfer and rearrangements are 2 more common mechanism patterns you will face in organic chemistry. This is in addition to Nucleophilic attack and Loss of Leaving Group discussed in Mechanism Video Part 1. You’ll see multiple proton transfer examples in action including turning a bad leaving group into a good leaving group! Rearrangement mechanism are broken down for […]
Ring Expansion via Hydride Shift and Methyl Shift
Ring expansions occur as a carbocation rearrangement when an unstable cycloalkane is near a carbocation. You will come across ring expansion mechanisms during alkene reactions and later in SN1 and E1 reactions. They key is to recognize when a ring is unstable, and the type of rearrangement that will help it become more stable. But don’t […]
SN1 Reaction Mechanism with Hydride Shift and Carbocation Rearrangement Part 3
SN1 SN2 E1 Series: Video 11 In this final SN1 video you’ll see tricky examples involving less substituted carbocation intermediates followed by carbocation rearrangements and hydride shifts. When working through these reactions pay special attention to the patterns that help determine the SN1 mechanism over a potential SN2 or E2 (Watch on YouTube: SN1 Part […]